
Welcome
We specialize in providing tailored security services, armed and unarmed, to ensure your specific security needs are met, regardless of the size or nature of your business. Our security services can be designed for optimal fit with your individual business requirements and security budgetary concerns. We have over 40 years of law enforcement experience.


INTEGRATED GUARDING
DPA Protective Agency, Inc., is able to provide armed and unarmed security solutions for both private and public sector organizations. We offers some of the following sevices: Security officers, Executive Protection, Parking lot security Enforcement & Patrols, Residential/ Gated community Patrols, Special Events, Vehicle Escorts, Tented House, Short/Long Term Project, Chauffeur Services, Private Party. If you require our Security Officer services, please call us now at (305) 910-9671 so we can analyze and customize your security needs.
Quote
EXECUTIVE PROTECTION
Our team works directly with the client to ensure the most advantageous method of protection, which may include the utilization of armed or unarmed guards in various methods.
Quote
TEMPORARY SECURITY
Permanent, Temporary and Emergency Guard Coverage; a Security Officer is posted on your site to perform patrol, protection and surveillance.
Quote
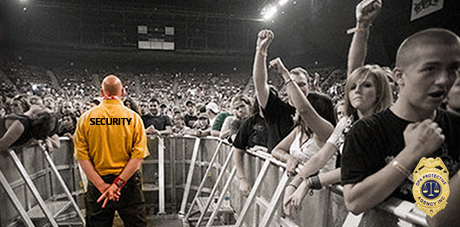
SPECIAL EVENT SECURITY
Procedures are developed with your input and our team to ensure the safety and wellbeing.
Quote

LUXURY LIVING
The Security Officer, aside from deterring crime through presence alone, will observe and report any violations of law, enforce rules, regulations and covenants of your property.
Quote
Copyright © 2014. DPA Protective Agency, Inc.
701 Brickell Ave, Suite 1550FL,Miami, Florida 33131 33166
Phone:305.910.9671
www.dpaprotection.com – Powered by: Internet Marketing Agency.
